三角形OABの面積 < 扇型OABの面積 < 三角形OACの面積　より \( \dfrac{1}{2} \cdot r \cdot r\sin{x} \ \lt \ \dfrac{1}{2} \cdot r \cdot \ rx \ \lt \ \dfrac{1}{2} \cdot r \cdot r\tan{x} \)
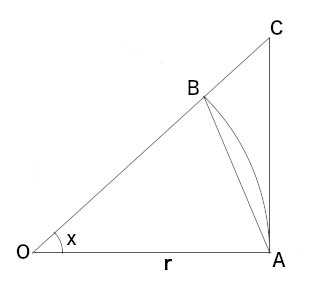
整理すると \( \sin{x} \lt x \lt \tan{x} \) ... ①
①の各辺を \( \sin{x} \) で割ると \( 1 < \dfrac{x}{ \sin{x} } < \cos{x} \)
\( \displaystyle \lim_{ x \to 0 } \cos{x} = 1 \) だから \( \displaystyle \lim_{ x \to 0 } \dfrac{x}{ \sin{x} } = 1 \) となる。

また ①の逆数をとると \( \cot{x} \lt \dfrac{1}{x} \lt \dfrac{1}{ \sin{x} } \)
各辺に \( \sin{x} \) をかけると \( \cos{x} \lt \dfrac{ \sin{x} }{x} \lt 1 \)
だから \( \displaystyle \lim_{ x \to 0 } \dfrac{ \sin{x} }{x} = 1 \) となる。

ロピタルの定理 $$ \lim_{x \to 0} \frac{f(x)}{g(x)} = \lim_{x \to 0} \frac{f'(x)}{g'(x)} $$